Movimiento Circular Uniforme

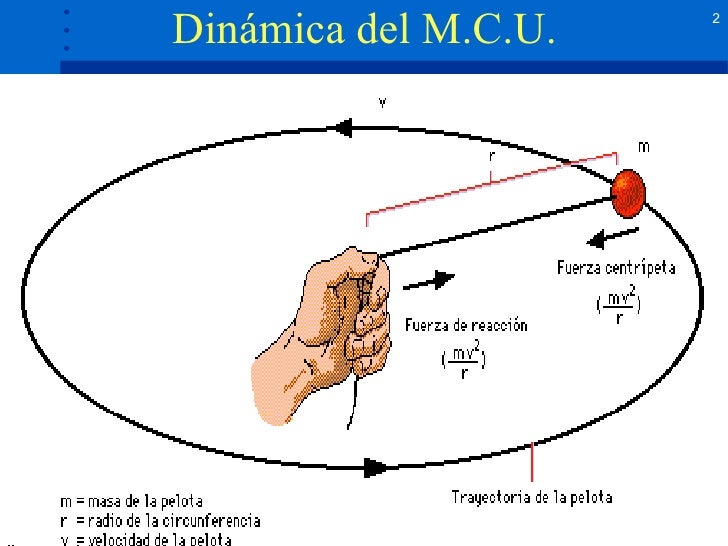
La Naturaleza y tu día a día están llenos de ejemplos de movimientos circulares uniformes (m.c.u.). La propia Tierra es uno de ellos: da una vuelta sobre su eje cada 24 horas. Los viejos tocadiscos o un ventilador son otros buenos ejemplos de m.c.u. Un cuerpo realiza un movimiento circular uniforme (m.c.u.) cuando su trayectoria es una circunferencia y su velocidad angular es constante. En este apartado vamos a estudiar.

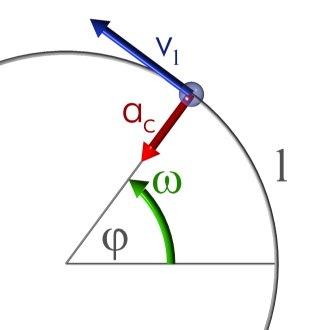
El movimiento circular uniforme (m.c.u.) es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales. En él, el vector velocidad no cambia de módulo pero sí de dirección (es tangente en cada punto a la trayectoria). Esto quiere decir que no tiene aceleración tangencial ni aceleración angular,  aunque sí aceleración normal.

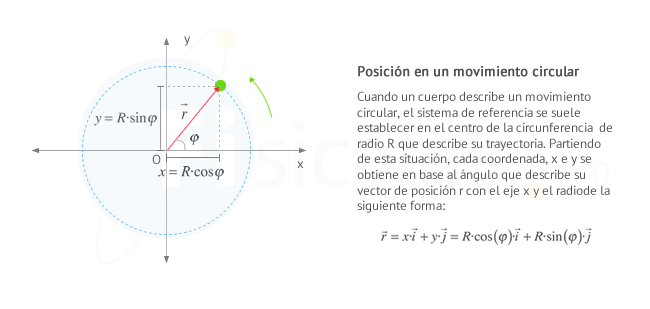
Eligiendo el origen de coordenadas para estudiar el movimiento en el centro de la circunferencia, y conociendo su radio R, podemos expresar el vector de posición en la forma:

r⃗ =x⋅i⃗ +y⋅j⃗ =R⋅cos(φ)⋅i⃗ +R⋅sin(φ)⋅j⃗ 

De esta manera, la posición y el resto de magnitudes cinemáticas queda definida por el valor de φ en cada instante.

Algunas de las características de este movimiento:

1. La velocidad angular es constante (ω = cte)
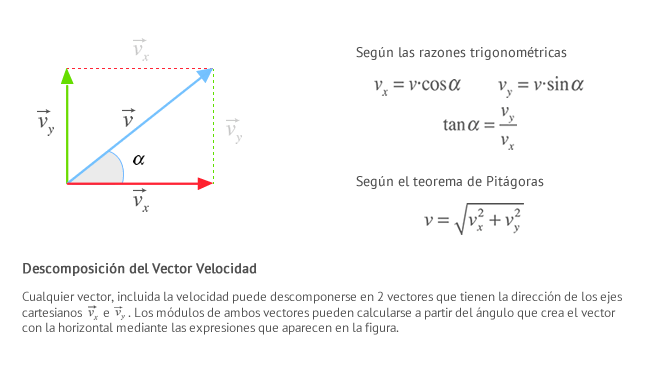
2. El vector velocidad es tangente en cada punto a la trayectoria y su sentido es el del movimiento. Esto implica que el movimiento cuenta con aceleración normal
3. Tanto la aceleración angular (α) como la aceleración tangencial (at) son nulas, ya que que la rapidez o celeridad (módulo del vector velocidad) es constante
4. Existe un periodo (T), que es el tiempo que el cuerpo emplea en dar una vuelta completa. Esto implica que las características del movimiento son las mismas cada T segundos. La expresión para el cálculo del periodo es T=2π/ω y es sólo válida en el caso de los movimientos circulares uniformes (m.c.u.)
5. Existe una frecuencia (f), que es el número de vueltas que da el cuerpo en un segundo. Su valor es el inverso del periodo.

En la gráfica aparece un cuerpo realizando un movimiento circular uniforme.

Arrastra el valor de la rapidez (módulo del vector velocidad)  para observar como el cuerpo se mueve más deprisa o más despacio.

Observa las distintas magnitudes cinemáticas. Comprueba además, que el vector velocidad, en verde, es tangente en cada punto a la trayectoria y por otro lado, la aceleración normal, en rojo, es la responsable de que cambie la dirección de la velocidad. Su dirección apunta siempre hacia el centro del radio de giro y su valor (módulo) depende de la rapidez que tenga el cuerpo.

Longitud de arco y Ángulo de la trayectoría circular

Siendo r el radio de la trayectoria circular y n el número de vueltas

Longitud de arco (∆s)

Ángulo barrido por la trayectoria (ɸ):

Podemos escribir relacionando el arco y el ángulo:

 Unidades

• Las unidades del arco: son el metro (m) , múltiplos y submúltiplos, o cualquier unidad que corresponda a la unidad de longitud.

• Las unidades de ángulo 
  

Velocidad Tangencial

Se observa en la figura, que la velocidad del móvil no es constante, sino que su dirección está cambiando. Pero la rapidez es constante ya que recorre arcos iguales en intervalos de tiempo iguales.

Entonces podemos calcular la rapidez Tangencial:

La rapidez tangencial es tangente al punto en un instante y tiene la dirección y sentido de instante.

Además es llamada, velocidad lineal o circunferencial

Velocidad angular

 En el movimiento Circular podemos calcular otro tipo de velocidad que llamamos velocidad angular (ω).

Es el ángulo (ɸ) que berre en unidad de tiempo (t).

En el M.C.U.al igual que la rapidez tangencial la velocidad angular es constante.

La unidad de la velocidad angular es radianes/segundos = rad/s.

En el caso que se trabaje la ecuación con 360°  la unidad de la velocidad angular es grados/segundos =º/s

La dirección y sentido de la velocidad angular

La velocidad angular es una magnitud vectorial.

La característica de la dirección y sentido del vector que lo representa son:

Dirección es el eje de rotación del cuerpo en movimiento

Sentido se determina mediante una regla convencional de la mano derecha

Se supone el eje de rotación tomado con la mano derecha, de tal manera que los dedos de la mano indiquen el sentido de la rotación del cuerpo. El pulgar extendido indicara el sentido de la velocidad angular ω.

Comparación entre Velocidad Tangencial y Velocidad Angular

Si observamos la figura

quiere decir que B recorre mayor arco que A en el mismo intervalo de tiempo, entonces:

Sin embargo, el ángulo barrido  por el cuerpo A y por el cuerpo B es el mismo en unidad de tiempo:

 Se concluye. Si un objeto rota alrededor de un eje fijo, todos los puntos tienen la misma rapidez angular. En cambio, la rapidez tangencial de un punto dependerá del radio.

Relación entre velocidad tangencial y angular

Las ecuaciones de rapidez tangencial y angular son respectivamente:

Relacionamos las dos ecuaciones dividiendo una con otra y de esa relación resulta

De donde

Período de un movimiento circular

En el caso que estamos tratando (movimiento circular), el período (T) es el tiempo que tarda el móvil en dar una vuelta.

Se calcula dividiendo el tiempo (t) entre el número de vueltas(n) que las realizó en dicho tiempo.

Frecuencia de un movimiento circular

La frecuencia (f) es el número de vueltas dadas en unidad de tiempo.

Se calcula dividiendo el número de vueltas(n) entre el tiempo (t) que las realizó.

 En el sistema internacional de medidas, se expresa en hertz, que equivale a

Movimiento Parabólico

Se denomina movimiento parabólico al realizado por cualquier objeto cuya trayectoria describe una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a un campo gravitatorio uniforme. El movimiento parabólico es un ejemplo de un movimiento realizado por un objeto en dos dimensiones o sobre un plano. Puede considerarse como la combinación de dos movimientos que son un movimiento horizontal uniforme y un movimiento vertical rectilíneo.

Las ecuaciones del movimiento parabólico son:

• Las ecuaciones del m.r.u. para el eje x
  x=x0+vx⋅t
  ​
• Las ecuaciones del m.r.u.a. para el eje y
  vy=v0y+ay⋅t
  y=y0+v0y⋅t+12⋅ay⋅t2

Dado que, como dijimos anteriormente, la velocidad forma un ángulo α con la horizontal, las componentes x e yse determinan recurriendo a las relaciones trigonométricas más habituales:

Finalmente, teniendo en cuenta lo anterior, que y0 = H , x0 = 0, y que ay = -g , podemos reescribir las fórmulas tal y como quedan recogidas en la siguiente lista. Estas son las expresiones finales para el cálculo de lasmagnitudes cinemáticas en el movimiento parabólico o tiro oblicuo:

• Posición (m)
  • Eje horizontal
    x=vx⋅t=v0⋅cos(α)⋅t
  • Eje vertical
    y=H+v0y⋅t−12⋅g⋅t2=H+v0⋅sin(α)⋅t−12⋅g⋅t2
• Velocidad (m/s)
  • Eje horizontal
    vx=v0x=v0⋅cos(α)
  • Eje vertical
    vy=v0y−g⋅t=v0⋅sin(α)−g⋅t
• Aceleración (m/s2)
• Eje horizontal
  ax=0
• Eje vertical
  ay=−g

Ecuación de posición y de trayectoria en el movimiento parabólico

La ecuación de proyección de un cuerpo nos sirve para saber en qué punto se encuentra en cada instante de tiempo. En el caso de un cuerpo que se desplaza en dos dimensiones, recuerda que, de forma genérica, viene descrita por:

r⃗ (t)=x(t)i⃗ +y(t)j⃗ 

Sustituyendo la expresiones anteriores de la posición en el eje horizontal ( m.r.u. ) y en el eje vertical ( m.r.u.a. ) en la ecuación de posición genérica, podemos llegar a la expresión de la ecuación de posición para el lanzamiento horizontal.

La ecuación de posición del movimiento parabólico viene dada por:

r⃗ =(x0+v0x⋅t)⋅i⃗ +(H+v0y⋅t−12⋅g⋅t2)⋅j⃗ 

Por otro lado, para saber qué trayectoria sigue el cuerpo, es decir, su ecuación de trayectoria, podemos combinar las ecuaciones anteriores para eliminar t, quedando:

y=H+v0y⋅(xv0x)−12⋅g⋅(xv0x)2=H+k1⋅x−k2⋅x2k1=v0yvx;k2=12⋅v0x2⋅g

Como cabía esperar, se trata de la ecuación de una parábola.

Por otro lado, será frecuente que en los ejercicios te pidan alguno de los siguientes valores.

Altura máxima

Este valor se alcanza cuando la velocidad en el eje y, vy , vale 0. A partir de la ecuación de velocidad en el eje vertical, e imponiendo vy = 0, obtenemos el tiempo t que tarda el cuerpo en llegar a dicha altura. A partir de ese tiempo, y de las ecuaciones de posición, se puede calcular la distancia al origen en el eje x y en el eje y.

Tiempo de vuelo

Se calcula igualando a 0 la componente vertical de la posición. Es decir, el tiempo de vuelo es aquel para el cual la altura es 0 (se llega al suelo).

Alcance

Se trata de la distancia máxima en horizontal desde el punto de inicio del movimiento al punto en el que el cuerpo impacta el suelo. Una vez obtenido el tiempo de vuelo, simplemente sustituye en la ecuación de la componente horizontal de la posición.

Ángulo de la trayectoria

El ángulo de la trayectoria en un determinado punto coincide con el ángulo que el vector velocidad forma con la horizontal en ese punto. Para su cálculo obtenemos las componentes vx y vy y gracias a la definición trigonométrica de tangente de un ángulo, calculamos α:

tan(α)=catetoopuestocatetocontiguo=vyvx⇒α=tan−1(vyvx)