Los Vectores en el Espacio

Por medio de la Geometría euclidiana o Parabólica (Es la que estudia las propiedades del plano y el espacio tridimensional) postulado por Euclides en su libro "Los Elementos; el Matemático, Físico y Astrónomo Irlandés William Rowan Hamilton planteó diversos temas incluyendo como herramienta principal a los vectores para resaltar su uso y darle sentido a algunas incógnitas que nos podría agobiar.

Un vector esta definido como un segmento de recta dirigido en el espacio o una magnitud física definida en un sistema de referencia que a su vez esta comprendido por: EL origen, también denominado punto de aplicación, es el punto exacto en donde actúa el vector; Módulo, éste es la longitud o tamaño del vector. Para hallarla es preciso conocer el origen y el extremo del vector, pues para saber cuál es el módulo del vector, debemos medir desde su origen hasta su extremo;La dirección, viene dada por la orientación en el espacio de la recta que lo contiene; El sentido, es el que indica mediante una punta de flecha situada en el extremo del vector, indicando hacia qué lado de la línea de acción se dirige el vector.

Hay que tener muy en cuenta el sistema de referencia de los vectores ,que estará formado por un origen y tres ejes perpendiculares. Este sistema de referencia permite fijar la posición de un punto cualquiera con exactitud.

Suma y resta de vectores

La suma de dos vectores libres es otro vector libre que se determina de la siguiente forma:

Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo.

Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores.

Para efectuar sumas o restas de tres o más vectores, el proceso es idéntico. Basta con aplicar la propiedad asociativa.

Al vector que se obtiene al sumar o restar varios vectores se le denomina resultante.

 Producto de un vector por un escalar

El resultado de multiplicar un escalar k por un vector v, expresado analíticamente por kv, es otro vector con las siguientes características :

1.- Tiene la misma dirección que v.
2.- Su sentido coincide con el de v, si k es un número positivo, y es el opuesto, si k es un número negativo.
3.- El módulo es k veces la longitud que representa el módulo de v. ( Si k es 0 el resultado es el vector nulo).

Analíticamente, tenemos que multiplicar el escalar por cada una de las coordenadas del vector.

Producto escalar de dos vectores

El producto escalar de dos vectores, expresado analíticamente 

como r · v, se obtiene de la suma de los productos formados por las componentes de uno y otro vector. Es decir, dados dos vectores r y v, expresados en un mismo sistema de coordenadas:

r = rxi + ryj + rzk

v = vxi + vyj + vzk  

el resultado de multiplicar escalarmente r por v es:

r · v = rx· vx + ry · vy+ rz · vz

Esta operación no solo nos permite el cálculo de la longitud de los segmentos orientados que representan ( sus módulos ), sino también calcular el ángulo que hay entre ellos. Esto es posible, ya que el producto escalar también se puede hallar en función de sus módulos y del coseno del ángulo que forman.

Producto vectorial

El producto vectorial de los vectores a y b, se define como un vector, donde su dirección es perpendicular al plano de a y b, en el sentido del movimiento de un tornillo que gira hacia la derecha por el camino más corto de a a b,

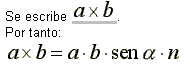
donde n es un vector unitario perpendicular al plano de a y b en el sentido del movimiento de un tornillo que gira hacia la derecha de a a b.

Propiedades:

Módulo de un vector

Un vector no solo nos da una dirección y un sentido, sino también una magnitud, a esa magnitud se le denomina módulo.

Gráficamente: es la distancia que existe entre su origen y su extremo.

Para hallar el modulo de un vector aplicamos la siguiente formula, obtenida del teorema de Pitágoras