Movimiento Rectilineo Uniformemente Acelerado
El movimiento rectilíneo uniformemente acelerado (m.r.u.a.), también conocido como movimiento rectilíneo uniformemente variado (m.r.u.v), es un movimiento rectilíneo con aceleración constante, y distinta de cero.
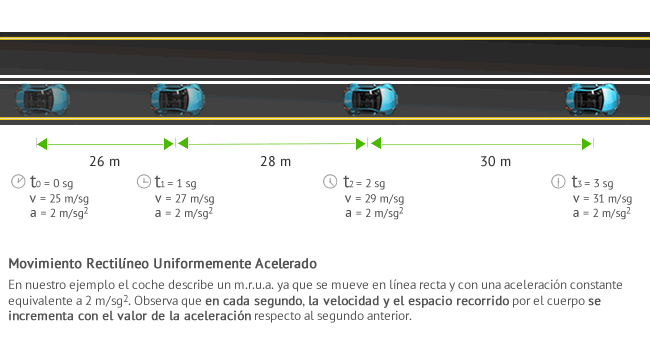
El movimiento rectilíneo uniformemente aceleradoes un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.
Este es el significado del movimiento uniformemente acelerado, el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.
En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.
En este movimiento la velocidad es variable, nunca permanece constante; lo que si es constante es la aceleración.
Entenderemos como aceleración la variación de la velocidad con respecto al tiempo. Pudiendo ser este cambio en la magnitud(rapidez), en la dirección o en ambos.
Las ecuaciones del movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) son:
Donde:
- x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
- v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional es el metro por segundo (m/s)
- a: La aceleración del cuerpo. Permanece constante y con un valor distinto de 0. Su unidad en el Sistema Internacional es el metro por segundo al cuadrado (m/s2)
- t: El intervalo de tiempo estudiado. Su unidad en el Sistema Internacional es el segundo (s)
Aunque las anteriores son las ecuaciones principales del m.r.u.a. y las únicas necesarias para resolver los ejercicios, en ocasiones resulta útil contar con la siguiente expresión:
En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s2. ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?
Veamos los datos que tenemos:
Conocemos tres de las cinco variables, entonces, apliquemos las fórmulas: Averigüemos primero la distancia que recorrerá durante los 20 segundos:
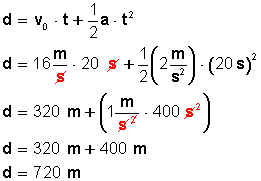
Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:



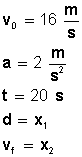
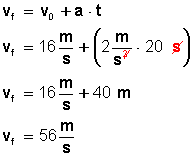
No hay comentarios:
Publicar un comentario